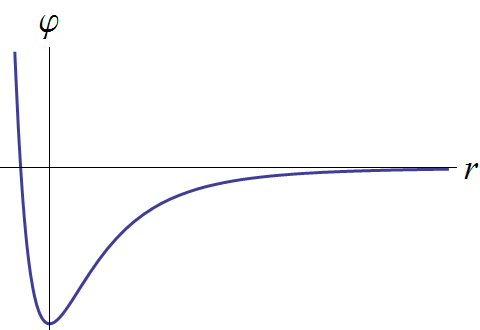
Interatomic Potemtials.
A significant part of my present research interests lies in interatomic potentials development.Quantum-mechanical models of atomistic and molecular properties are often too expensive in many applications. Empirical models (atomistic or continuum), on the other hand, offer only a qualitative accuracy. The goal of my research is to take the best of these two worlds: to design models that are as efficient as the empirical ones while as accurate as the quantum-mechanical ones.
 |
Interatomic Potemtials. A significant part of my present research interests lies in interatomic potentials development. |
Atomistic-to-Continuum Coupling. Much of my past research concerned the Atomistic-to-Continuum (AtC) coupling method (also known as a quasicontinuum class of methods)—a particular form of spatial coarse-graining for crystals. [details and publications on the AtC coupling] |
 |